任意の画像を数式で表現する
WolframAlphaで「Popular Curves」などと検索をかけると、ロゴや食品をはじめ、アニメキャラクターや実在する人物までを媒介変数表示された曲線で表している作品が多く見受けられる。下の画像はアインシュタインのプロットらしい。
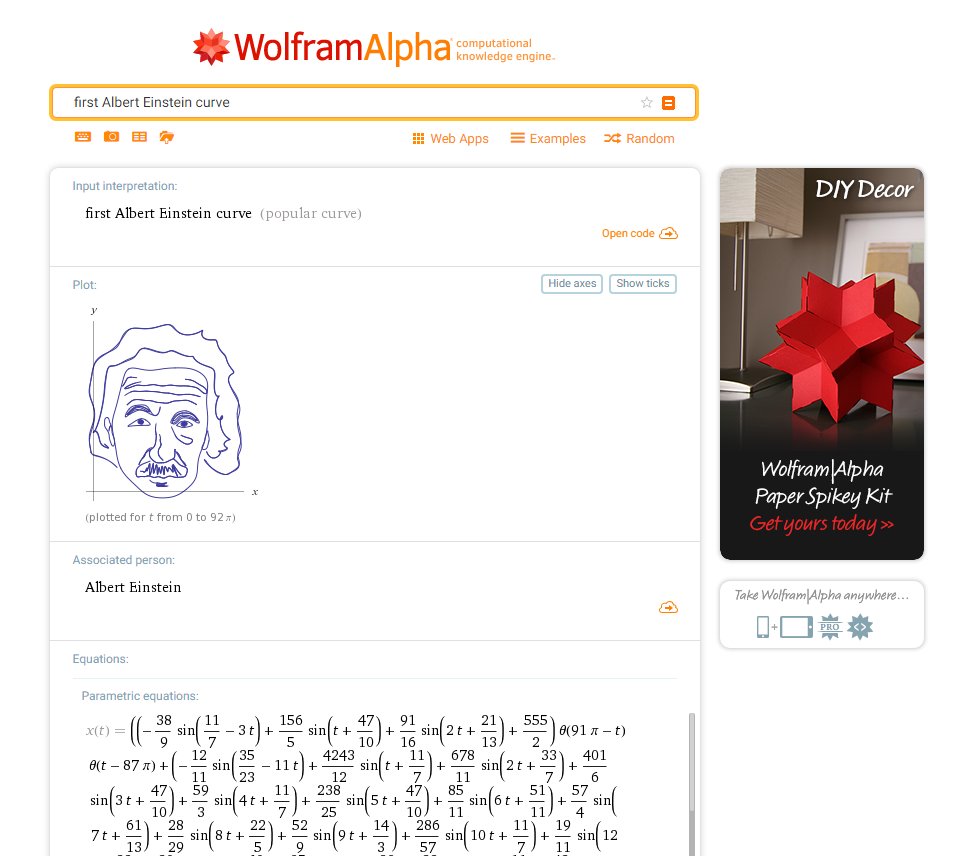
このように、任意の画像を数式で表現する方法については、以下のリンクに詳しい記載がある。 aomoriringo.hateblo.jp
しかし、上記のサイトは有償ソフトウェアたるMathematicaを利用しているためハードルが高い。そこで、Mathematicaを購入することなく利用する方法を解説した下記のサイトを参考にし、両者を組み合わせることによって画像の数式表現を実現したログを残しておこうと思う。
hirax.net::「Wolfram CDF PlayerをMathematicaとして使う方法」をRubyでもっと簡単にしてみた
なお、以下の作業はWindows10上で行っており, 全体を通じてブラウザはFirefoxを利用している。他のブラウザを使用していて動かない場合は変更を検討してみると良いかもしれない。
A. Mathematicaを利用できる環境を整える
Mathematica自体は有料だが、Mathematicaにより生成されたCDFファイルを再生する「wolfram CDF player」は無料配布されている(MathematicaとCDF playerの関係についてはこちらを参照願いたい)。今回はこれとRubyのWebサーバーを組み合わせることにより実行環境を構築することとする。
wolfram CDF playerの入手
まずは以下のURLからこれを入手しよう。ダウンロード・インストールにそれなりに時間がかかるので注意。
Ruby実行環境の構築
こちらを参考にRubyのセットアップをしよう。以下のURLからRubyのインストーラをダウンロードして実行すれば簡単にインストールすることができる。個人的にはパスも通しておいた方が何かと便利なのではないかと思う。
それでは、早速冒頭で述べた記事に記載のrubyコードをコピペして適当なディレクトリに"math.rb"などどして保存し、コマンドプロンプトで
ruby math.rb
と実行してみる。Windows10ではここで警告が出たが適当にOKしておこう。なお、このサーバーを終了させるにはhttp://localhost/shutdownにアクセスすればよい(ブラウザにお気に入り登録しておくと便利かもしれない)。
長い文字列を送信できるようにしておく
以下の作業で、WEBから一定以上の数の文字列を送信した場合に「ERROR WEBrick::HTTPStatus::RequestURITooLarge」というエラーメッセージが生じて送信が失敗する場合がある。その場合、こちらを参考に、C:\Ruby23-x64\lib\ruby\2.3.0\webrickに存在するhttprequest.rbをテキストエディタで開き、MAX_URI_LENGTHを指定している箇所を
MAX_URI_LENGTH = 64 * 1024 * 1024 # :nodoc:
などと変更し上書き保存することでこのエラーに備えておくことができる。
Universal Mathematica Manupulator 3 にアクセス
上のRuby Webサーバーを立ち上げた状態で、ブラウザでUniversal Mathematica Manipulator 3にアクセスする。初回のアクセス時に「umm3.cdfをダウンロードしますか」というようなことを訊かれるので適当なディレクトリにダウンロードしておく。上手く行っていれば暫く待っていると下図のような立体が右側領域に表示されるはずである。
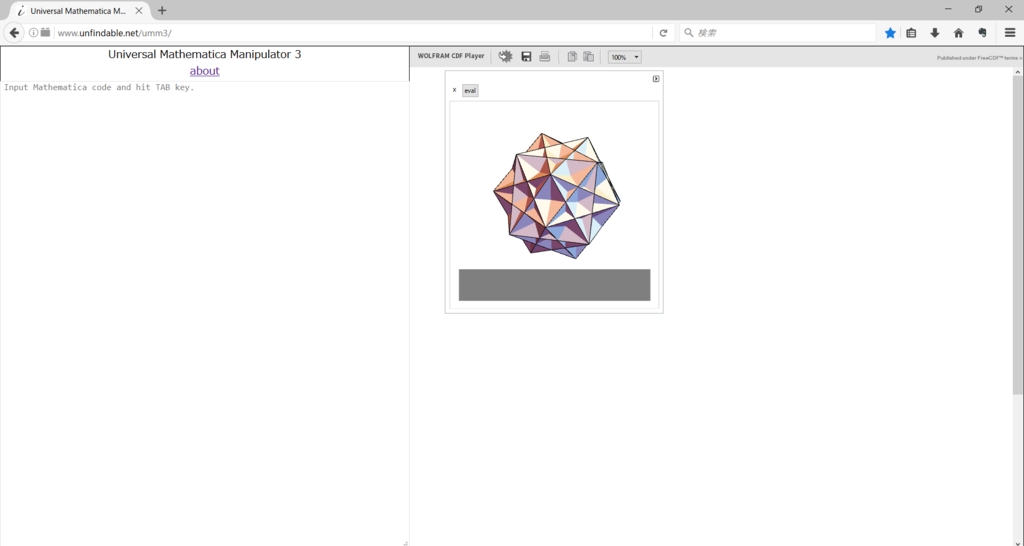
※「クラッシュしました」といったメッセージが時たま表示されるが、ブラウザやあるいはPCごと再起動してみたりを何回か行えば(?)復旧する。この辺のことは全然分からないので詳しい方はぜひ教えてほしい。
使い方としては、まず左側に数式を打ち込んだ状態でTABキーを押して(入力内容がRubyのWebサーバーに送信される)、その後右側領域のevalボタンを押せば出力が表示される、という流れである。例えば左側に「1+1」を入力して上記の作業を行った場合、右側には2が表示される。
B. 実際に画像を数式化してみる
注:以下に示すコードは、これも最初に述べた記事に載っているものを一部改変しただけでほとんどコピペである。
今回は、主に筆者がスピッツファンだという理由によりスピッツのロゴを数式で表現してみようと思う。画像のローカルのパスを渡すことによりインポートすることも少なくともデスクトップ版Mathematicaでは可能なようだが、今回は上手くいかなかった(?)

関数の読み込みと画像の取り込み
最初に指定されているmaxOrderNumが使用する数式の最大次数となる。
(* parameters *) (* 最大次数 *) maxOrderNum = 200; (* 画像URL, もしくはローカルパス *) imageURL = "https://yt3.ggpht.com/-wbOANd5n5ZY/AAAAAAAAAAI/AAAAAAAAAAA/ELOj6QE_dyc/s900-c-k-no-mo-rj-c0xffffff/photo.jpg"; pointListToLines[pointList_, neighbothoodSize_: 6] := Module[{L = DeleteDuplicates[pointList], NF, lambda, lineBag, counter, seenQ, sLB, nearest, nearest1, nextPoint, couldReverseQ, d, n, s}, NF = Nearest[L]; lambda = Length[L]; Monitor[ (*list of segments *) lineBag = {}; counter = 0; While[counter < lambda, (*new segment*) sLB = {RandomChoice[DeleteCases[L, _?seenQ]]}; seenQ[sLB[[1]]] = True; counter++; couldReverseQ = True; (*complete segment*) While[ (nearest = NF[Last[sLB], {Infinity, neighbothoodSize}]; nearest1 = SortBy[DeleteCases[nearest, _?seenQ], 1. EuclideanDistance[Last[sLB], #] &]; nearest1 =!= {} || couldReverseQ), If[ nearest1 === {}, (*extend the other end; penalize sharp edges*) sLB = Reverse[sLB]; couldReverseQ = False, (* prefer straight continuation *) nextPoint = If[Length[sLB] <= 3, nearest1[[1]], d = 1. Normalize[(sLB[[-1]] - sLB[[-2]]) + 1/2 (sLB[[-2]] - sLB[[-3]])]; n = {-1, 1} Reverse[d]; s = Sort[{Sqrt[(d.(# - sLB[[-1]]))^2 + (*perpendicular *)2 (n. (# - sLB[[-1]]))^2], #} & /@ nearest1]; s[[1, 2]]]; AppendTo[sLB, nextPoint]; seenQ[nextPoint] = True; counter++]]; AppendTo[lineBag, sLB]]; (*return segments sorted by length*) Reverse[SortBy[Select[lineBag, Length[#] > 12 &], Length]], (*monitor progress*) Grid[ {{Text[Style["progress point joining", Darker[Green, 0.66]]], ProgressIndicator[counter/lambda]}, {Text[Style["number of segments", Darker[Green, 0.66]]], Length[lineBag] + 1}}, Alignment -> Left, Dividers -> Center]]] (* Fourier coefficients of a single curve *) fourierComponentData[pointList_, nMax_, op_] := Module[{epsilon = 10^-3, myu = 2^14, M = 10000, s, scale, delta, L, nds, sMax, if, xyFunction, X, Y, XFT, YFT, type}, (* prepare curve *) scale = 1. Mean[Table[ Max[fl /@ pointList] - Min[fl /@ pointList], {fl, {First, Last}}]]; delta = EuclideanDistance[First[pointList], Last[pointList]]; L = Which[ op === "Closed", type = "Closed"; If[First[pointList] === Last[pointList], pointList, Append[pointList, First[pointList]]], op === "Open", type = "Open"; pointList, delta == 0., type = "Closed"; pointList, delta/scale < op, type = "Closed"; Append[pointList, First[pointList]], True, type = "Open"; Join[pointList, Rest[Reverse[pointList]]]]; (*re-parametrize curve by arclength *) xyFunction = BSplineFunction[L, SplineDegree -> 4]; nds = NDSolve[ {s'[t] == Sqrt[xyFunction'[t].xyFunction'[t]], s[0] == 0}, s, {t, 0, 1}, MaxSteps -> 10^5, PrecisionGoal -> 4]; (* total curve length *) sMax = s[1] /. nds[[1]]; if = Interpolation[ Table[{s[rho] /. nds[[1]], rho}, {rho, 0, 1, 1/M}]]; X[t_Real] := BSplineFunction[L][Max[Min[1, if[(t + Pi)/(2 Pi) sMax]], 0]][[1]]; Y[t_Real] := BSplineFunction[L][Max[Min[1, if[(t + Pi)/(2 Pi) sMax]], 0]][[2]]; (* extract Fourier coefficients *) {XFT, YFT} = Fourier[Table[#[N@t], {t, -Pi + epsilon, Pi - epsilon, (2 Pi - 2 epsilon)/myu}]] & /@ {X, Y}; {type, 2 Pi/ Sqrt[myu]*((Transpose[ Table[{Re[#], Im[#]} &[Exp[I k Pi] #[[k + 1]]], {k, 0, nMax}]] & /@ {XFT, YFT}))}] Options[fourierComponents] = {"MaxOrder" -> maxOrderNum, "OpenClose" -> 0.025}; fourierComponents[pointLists_, OptionsPattern[]] := Monitor[ Table[fourierComponentData[ pointLists[[k]], If[Head[#] === List, #[[k]], #] &[OptionValue["MaxOrder"]], If[Head[#] === List, #[[k]], #] &[OptionValue["OpenClose"]] ], {k, Length[pointLists]}], Grid[ {{Text[ Style[ "progress calculating Fourier coefficients", Darker[Green, 0.66]]], ProgressIndicator[k/Length[pointLists]]}}, Alignment -> Left, Dividers -> Center]] /; Depth[pointLists] === 4 makeFourierSeries[ {"Closed" | "Open", {{cax_, sax_}, {cay_, say_}}}, t_, n_] := {Sum[If[k == 0, 1/2, 1] cax[[k + 1]] Cos[k t] + sax[[k + 1]] Sin[k t], {k, 0, Min[n, Length[cax]]}], Sum[If[k == 0, 1/2, 1] cay[[k + 1]] Cos[k t] + say[[k + 1]] Sin[k t], {k, 0, Min[n, Length[cay]]}]} (* 画像読み込み *) img = Import[imageURL];
これをAで準備したUniversal Mathematica Manipulator 3の左側領域にコピペして実行する(NULLと表示されるはずである)。
エッジを抽出し線分の数を表示
(* エッジ抽出 *) edgeImage = Thinning[EdgeDetect[ColorConvert[ ImagePad[Image[Map[Most, ImageData[img], {2}]], 20, White], "Grayscale"]]]; edgePoints = {#2, -#1} & @@@ Position[ImageData[edgeImage], 1, {2}]; SeedRandom[2]; hLines = pointListToLines[edgePoints, 16]; (* 線分の数を表示 *) Length[hLines]
これを実行し暫く待つと右側に線分の数が表示される。今回使用したスピッツのロゴの場合は3であった。
エッジ抽出の結果を描画してみる
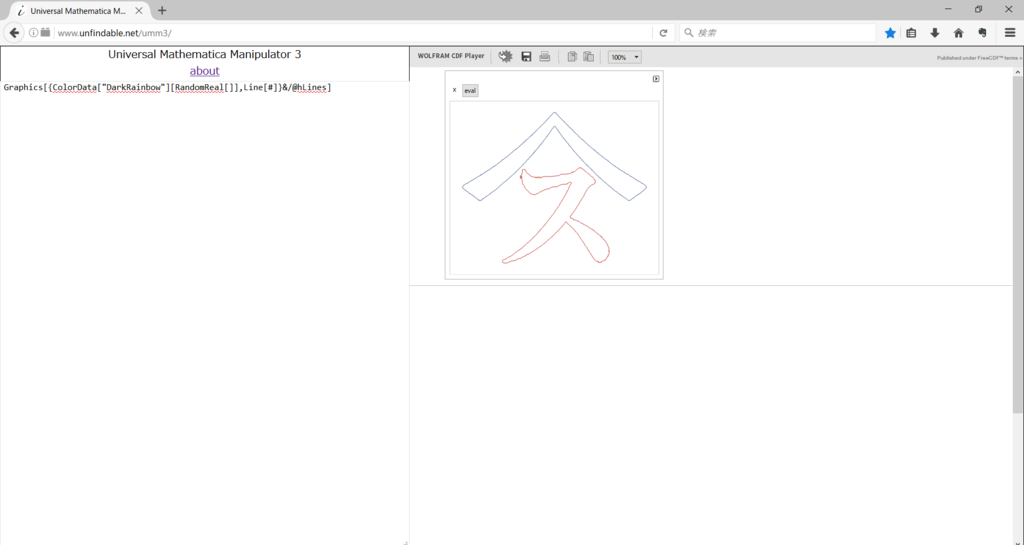
Graphics[{ColorData["DarkRainbow"][RandomReal[]],Line[#]}&/@hLines]
実行結果は下図のようになった。
フーリエ変換を実行&数式を表示
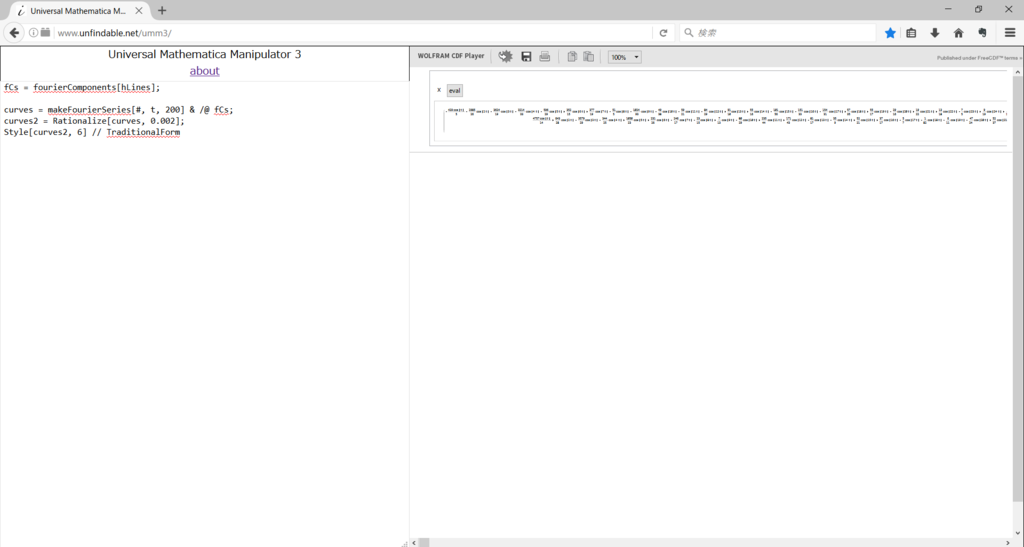
fCs = fourierComponents[hLines]; curves = makeFourierSeries[#, t, 200] & /@ fCs; curves2 = Rationalize[curves, 0.002]; Style[curves2, 6] // TraditionalForm
少し時間はかかるが、これでめでたく数式を得ることに成功する。 得られた数式はコピペでテキストファイルなどに保存することが可能である。